15 Reduction Techniques for Survival Analysis
This page is a work in progress and minor changes will be made over time.
In this part of the book we will introduce and formalize the concept of reduction techniques for survival analysis. A reduction is defined as “a complex problem decomposed into simpler subproblems so that a solution to the subproblems gives a solution to the complex problem” (Beygelzimer et al. 2016). Reduction techniques discussed here may introduce additional overhead, for example the need to perform a specific type of data pre-processing. However, they are still viewed as reductions as they reduce survival predictive problems to one or more regression and classification problems. Reduction techniques can therefore simplify the application of machine learning methods to survival analysis, particularly in situations where
- the interface of a machine learning method of choice is not designed to handle complex survival data (for example it expects a one dimensional vector as target variable, whereas survival outcomes are defined as tuples of two or more elements).
- novel machine learning methods are often developed for classification or regression but without adaptations to survival analysis
- a particular extension of a machine learning method to survival analysis is restricted to a subset of relevant survival problems, often the single event, right-censored data setting.
It should be emphasized that the reductions discussed in this part of the book go beyond the simplistic and often erroneous reductions that can unfortunately be seen in some literature; for example, treating the event indicator as a target for a classification task or directly using the observed event time as a target for a regression task whilst ignoring the censoring status (Schwarzer, Vach, and Schumacher 2000). Instead, the reductions introduced here are valid methods for survival analysis that appropriately deal with censoring and/or truncation. The reductions introduced in this part of the book
- do not make (strong) assumptions about the underlying distribution of event times, and thus have the same advantages as non-parametric (Section 10.1) and semi-parametric methods (Section 10.2),
- are applicable to many survival tasks, including competing risks and multi-state settings (Chapter 4),
- can predict different quantities of interest, including (discrete) hazards, survival probabilities and cumulative incidence functions conditional on features,
- can use any off-the-shelf implementation of machine learning or deep learning methods for regression or classification (depending on the reduction technique),
- can (explicitly) model time-varying effects and thus deal with non-proportional hazards.
The general concept of reduction techniques is depicted in Figure 15.1 .
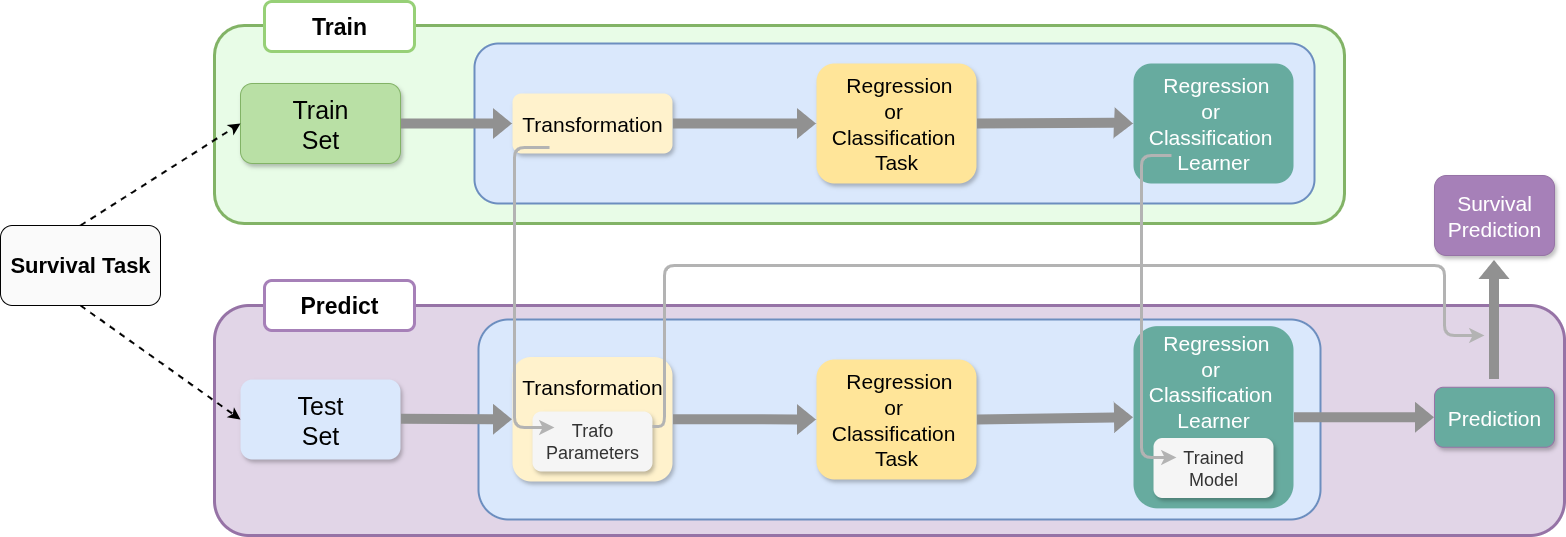
In the training phase, the data is transformed into a different format. The specifics of the transformation will depend on the reduction technique and the survival task at hand. Once the data is transformed, the target variable becomes a one-dimensional vector of a regression or classification task (again depending on the reduction technique). At this stage, a standard machine learning model for regression or classification can be applied to the transformed data without any additional changes to the model or its implementation.
In the prediction phase, if necessary, the test data is transformed into the same format as the training data (using the pre-specified or trained parameters of the data transformation during the training phase). This yields a data set which can be passed to the previously learned regression or classification model to generate predictions. Depending on the reduction technique and the quantity of interest, the predictions may need additional post-processing to obtain the desired survival quantity of interest.
In the following chapters we introduce specific reduction techniques. We differentiate between reductions that primarily aim to estimate a specific quantity of interest (like the survival probability) at one or few time points of the follow up, in particular IPC-weighted classification (Chapter 16) and pseudo-value based regression (Chapter 17), and partition-based reductions (Chapter 18) that aim to estimate the entire event time distribution, specifically the discrete-time approach (Section 18.2), survival stacking (Section 18.3) and the piecewise exponential models (Section 18.4). Finally, Chapter 19 introduces general concepts in order to apply machine learning methods to competing risks and multi-state tasks based on simpler single event learners.